Actuators and Sensors
| 1980 | 1990 | 2000 | 2010 |
| Emerging of PCs | Information superhighway | Human-center healthcare robotics |
| [VR Sph Motor] [Sph Wheel Motor] [3DOF Stage] [Sensors] [References] |
Biomechatronics
This research has been motivated by the role of dexterous actuators and sensors for measurement and control of high precision, intelligent machines for robotics and manufacturing automation [1]. Dr. Lee began his activities in the mid-1980 with contributions to the development of a three degrees-of-freedom (DOF) in-parallel wrist mechanism [2-4] and its micro-motion version driven by piezoelectric actuators [5], and an early (1988) proposal for a 3-DOF variable-reluctance stepper [6] as well as the first showing the important differences between the VRSM and the popular three-consecutive-joint wrist or spherical wrist motors of a different kind.
Variable Reluctance Spherical Motor (VRSM)
Dr. Lee and his students conducted some of the first detailed study on the creation of a three degrees of freedom (DOF) ball-joint-like variable-reluctance spherical motor (VRSM) to provide roll, yaw, and pitch motion in a single joint. This conceptualization of a VRSM, which eliminates constraints imposed by the tradition of three-consecutive-rotational-joints, has represented a significant breakthrough in new designs of multi-axes direct-drive systems that generate smooth, singularity-free, precision motion directly in the target direction in 3D space. This was followed by some of the first detailed studies provide a rational basis for the design [7-9], torque modeling and control strategies [10-12] (based on the concept of distributed, redundant actuation) and non-contact multi-DOF encoders for the VRSM, both theory and experimental validation.
|
|
 |
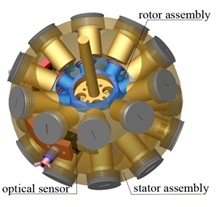

Around the-mid 2000s, Lee and his students have investigated the feasibility of designing a spherical wheel motor (SWM) [13] for applications (such as car wheels, propellers for boats, helicopter or underwater vehicle, gyroscopes, and machine tools) where dexterous orientation control of a continuously rotating shaft. Unlike a VRSM where the stator permanent magnets (PM) and the rotor electromagnets (EM) are placed on locations following the vertices of a regular polygon, equally-spaced magnetic poles are placed on layers of circular planes for a SWM. This enables the shaft to spin using a switching controller while allowing the shaft to incline much like a VRSM. A similar test-bed was developed in Singapore [14-15] for measuring the magnetic fields of the PM-based rotor and hence real-time computationof the Lorentz torque due to the current flow through the stator coils; validation of these meausred data against the method of magnetic field reconstruction using measured boundary conditions [16].
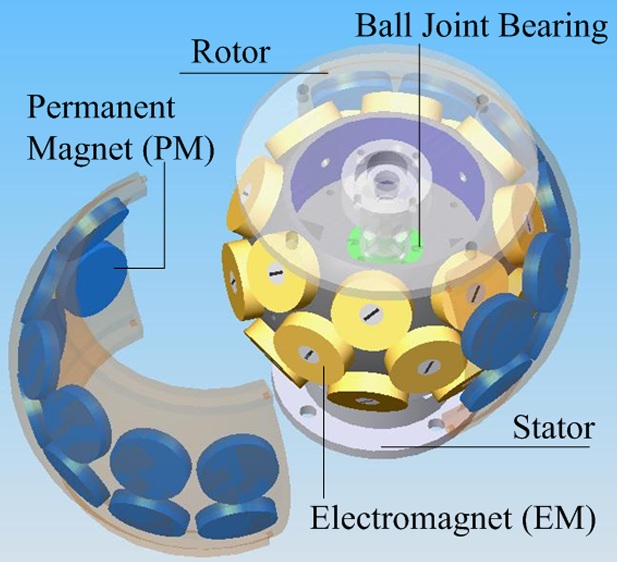 Unlike a VRSM or a SWM where the rotor PMs are embedded
in the “ball,” the PMs of the 3-DOF spherical orientation stage are housed
in the socket-like rotor assembly. Both forward and inverse torque models
are required in the design and control of a 3-DOF spherical orientation
stage. The forward model simulates the magnetic torque for a given set of
electrical inputs. The inverse model (required for both design analysis and
realtime control) computes an optimal set of electrical inputs todeliver the
specified torque. Two methods commonly used in calculating the forces
between stator EMs and rotor PMs of a spherical motor are the Lorentz force
equation and the Maxwell stress tensor. These methods require solving the
magnetic field and computing a volume or surface integral to derive the
force model. As general closed-form solutions are not available, the volume
or surface integrals are often solved numerically. Tthe interest to optimize
the design of task-oriented 3-DOF spherical motor has motivated us to
develop alternative techniques for analyzing magnetic fields and forces.
This effort has led to the method of distributed multipoles (DMP) [17] that
computes the 3-D magnetic field of a PM in a closed form. We further
proposed an improved method to derive an equivalent PM (ePM) such that the
magnetic field of the original ML EM can be characterized by DMP. With both
the PMs and EMs modeled as DMP, the magnetic forces on the system can be
calculated using the Maxwell stress tensor method or the dipole force
equation [18]. Unlike other commonly used methods that require to calculate
a time-consuming numerical (surface or volume) integral to derive the force,
the dipole-force equation (based on distributed dipoles replacing surface or
volume integrals by summations) offers closed-form solutions dramatically
reducing computation time by as much as four orders and has been validated
against known analytical solutions and experimental results.
Unlike a VRSM or a SWM where the rotor PMs are embedded
in the “ball,” the PMs of the 3-DOF spherical orientation stage are housed
in the socket-like rotor assembly. Both forward and inverse torque models
are required in the design and control of a 3-DOF spherical orientation
stage. The forward model simulates the magnetic torque for a given set of
electrical inputs. The inverse model (required for both design analysis and
realtime control) computes an optimal set of electrical inputs todeliver the
specified torque. Two methods commonly used in calculating the forces
between stator EMs and rotor PMs of a spherical motor are the Lorentz force
equation and the Maxwell stress tensor. These methods require solving the
magnetic field and computing a volume or surface integral to derive the
force model. As general closed-form solutions are not available, the volume
or surface integrals are often solved numerically. Tthe interest to optimize
the design of task-oriented 3-DOF spherical motor has motivated us to
develop alternative techniques for analyzing magnetic fields and forces.
This effort has led to the method of distributed multipoles (DMP) [17] that
computes the 3-D magnetic field of a PM in a closed form. We further
proposed an improved method to derive an equivalent PM (ePM) such that the
magnetic field of the original ML EM can be characterized by DMP. With both
the PMs and EMs modeled as DMP, the magnetic forces on the system can be
calculated using the Maxwell stress tensor method or the dipole force
equation [18]. Unlike other commonly used methods that require to calculate
a time-consuming numerical (surface or volume) integral to derive the force,
the dipole-force equation (based on distributed dipoles replacing surface or
volume integrals by summations) offers closed-form solutions dramatically
reducing computation time by as much as four orders and has been validated
against known analytical solutions and experimental results.
Sensors for Multi-DOF Spherical Motor and Orientation Stage
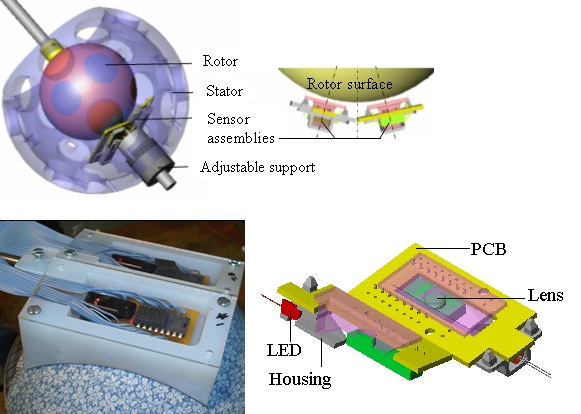 In
the early 1990s, Dr. Lee co-invented an image-reading system (see
Machine Vision), and with Parker [19] contributed
to the vision system modeling and methodology for designing efficient vision
systems that might otherwise require time-consuming and expensive physical
experimentation. The image-reading system has provided a basis for
developing a 3-DOF vision-based orientation sensor [20-21] that reads
encoded gridlines printed on a spherical surface. Lee and Zhou [22]
extended the vision-based method but used microscopic
surface
features (instead of dedicated pattern)
to determine motion
changes, which led to the design concept and theory of a dual-sensor system
capable of measuring 3-DOF planar and spherical motions in real time. The
concept feasibility of two prototype 3-DOF dual-sensor systems for measuring
the instantaneous center of rotation and the angular displacement of a
moving surface was demonstrated experimentally.
In
the early 1990s, Dr. Lee co-invented an image-reading system (see
Machine Vision), and with Parker [19] contributed
to the vision system modeling and methodology for designing efficient vision
systems that might otherwise require time-consuming and expensive physical
experimentation. The image-reading system has provided a basis for
developing a 3-DOF vision-based orientation sensor [20-21] that reads
encoded gridlines printed on a spherical surface. Lee and Zhou [22]
extended the vision-based method but used microscopic
surface
features (instead of dedicated pattern)
to determine motion
changes, which led to the design concept and theory of a dual-sensor system
capable of measuring 3-DOF planar and spherical motions in real time. The
concept feasibility of two prototype 3-DOF dual-sensor systems for measuring
the instantaneous center of rotation and the angular displacement of a
moving surface was demonstrated experimentally.
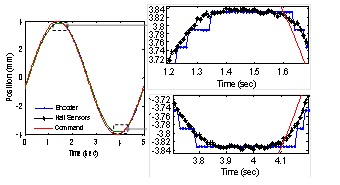
More recently, a novel method that determines the displacement and force/torque of a PM-based electromagnetic actuator using existing magnetic fields with low-cost Hall-effect sensors has been developed in [23]. Using a linear voice coil motor (VCM) as a platform for analysis, the experimental performance of a 9-sensor field-based system was compared against an optical encoder [24]. With a sinusoidal reference signal (0.2Hz frequency, 4mm amplitude), the corresponding positional estimate provided by the Hall-Effect sensors under PID control for one time period (shown below). The encoder controlled response follows a ‘staircase function’ (each step corresponds to the encoder resolution of 42.33μm) and is unable to adequately reproduce the peak and trough of the sinusoidal reference command. The field-based system, which by virtue of the analog outputs of the Hall-Effect sensors and continuous model of the ANN, permits interpolation between discrete training set points. This result in an overall smoother response as the field-based system is able to interpolate multiple data points within the encoder resolution as illustrated by the insets. In addition, while the actual peak and trough of the response can be inferred from the Hall-Effect sensors, the discrete nature of the encoder prevents a similar extraction. The demonstrated findings offer potentials in several other unique applications where magnetic fields play a role.
 |
 |
-
Vachtsevanos, G., K. Davey, and K-M. Lee, "On the Development of a Novel Intelligent Robotic Manipulator," IEEE Control Systems Magazine. June 1987, vol. 7, no. 3, pp. 9-15.
-
Lee, K-M. and D. Shah, "Kinematic Analysis of a Three-DOF In-parallel Actuated Manipulator," IEEE Trans. on Robotics and Automation. June 1988, vol. 4, issue 2, pp. 354-360.
-
Lee, K-M. and D. Shah, "Dynamic Analysis of a Three-DOF In-parallel Actuated Manipulator," IEEE Trans. on Robotics and Automation. June 1988, vol. 4, issue 2, pp. 361-367 .
-
Lee, K-M. and A. Chao, "On the Analysis of a Three-DOF Manipulator," Int. J. of Robotics and Automation. 1988, vol. 3, no. 2, pp. 90-96.
-
Lee, K-M. and S. Arjunan, "A Three-DOF Micro-motion In-Parallel Actuated Manipulator," IEEE Trans. on Robotics and Automation. October 1991, vol. 7, no. 5, pp. 634-641.
-
Lee, K-M. and C.-K. Kwan, "Design Concept Development of a Spherical Stepper for Robotic Applications," IEEE Trans. on Robotics and Automation. February 1991, vol. 7, no.1, pp. 175-180.
-
Lee, K-M., J. Pei, and R. Roth, "Kinematic Analysis of a Three-DOF VR Spherical Motor," Mechatronics. 1994, vol. 4, no. 6, pp. 581-605.
-
Zhou, Z. and K-M. Lee, "Characterization of a 3-DOF VR Spherical Motor," J. of Sys. Eng. 1994, vol. 4, pp. 60-69.
-
Roth, R. and K-M. Lee, "Design Optimization of a Three-DOF VR Spherical Motor," ASME J. of Engineering for Industry. August 1995, vol. 117, pp. 378-388.
-
Lee, K-M., R. Roth, and Z. Zhou, "Dynamic Modeling and Control of a Ball-joint-like VR Spherical Motor," ASME J. of Dynamic Systems, Measurement and Control. March 1996, vol. 118, no. 1, pp. 29-40.
-
Lee, K-M. D. E. Ezenekwe, and T. He, "Design and Control of a Spherical Air Bearing System for Multi-DOF Ball-joint-like Actuators," Mechatronics. 2003, vol. 13, pp. 175-194.
-
Lee, K.-M. R. A. Sosseh and Z. Wei, "Effects of the Torque Model on the Control of a VR Spherical Motor," IFAC J. of Control Engineering Practice. 2004, vol. 12, issue 11, pp. 1437-1449.
-
Lee, K.-M., H. Son, and J. Joni, "Concept Development and Design of a Spherical Wheel Motor (SWM)," Proc. of the 2005 IEEE ICRA, Barcelona, Spain, April 18-22,2005, pp. 3652- 3657.
-
Yan L., I. M. Chen, G. L. Yang, W. Lin and K. M. Lee, "Analytical and Experimental Investigation on the Magnetic Field and Torque of a Permanent Magnet Spherical Actuator," IEEE Trans. on Mechatronics. August 2006, vol. 11, no. 4, pp. 409-419.
-
Yan L., K.C. Lim, I. M. Chen, G. L. Yang, W. Lin and K. M. Lee, "Design and Analysis of a Permanent Magnet Spherical Actuator," IEEE Trans. on Mechatronics. April 2008, vol. 13, no. 2, pp. 239-248.
-
Hu, L., K.-M. Lee and X. Fu, "A Magnetic Field Reconstruction Method based on Measured Boundary Conditions for Electromagnetic Mechatronic Systems," IEEE/ASME Trans. on Mechatronics. Aug. 2010, vol. 15, no 4, pp. 595-602.
-
Son, H. and K.-M. Lee, "Distributed Multi-Pole Models for Design and Control of PM Actuators and Sensors," IEEE Trans. on Mechatronics. April 2008, vol. 13, no. 2, pp. 228-238.
-
Lee, K.-M., K. Bai, and J. Lim, "Dipole Models for Forward/Inverse Torque Computation of Spherical Motor," IEEE/ASME Trans. on Mechatronics. Feb 2009, vol 14, no. 1, pp 46-54.
-
Parker, J. and K-M. Lee, "Physically-Accurate Synthetic Images for Machine Vision Design," ASME J. of Manufacturing Science and Engineering. November 1999, vol. 121, no. 4, pp. 763-770.
-
Lee, K-M., G. Meyouhas, and R. Blenis, "A Machine-Vision-Based Wrist Sensor for Direct Measurement of Three-DOF Orientation," Mechatronics. 1993, vol. 3, no. 5, pp. 571-587.
-
Garner, H., M. Klement, and K-M. Lee, “Design and Analysis of an Absolute Non-Contact Orientation Sensor for Wrist Motion Control ,” Proc. of the IEEE/ASME AIM’01, Como, Italy, July 8–11 2001, pp. 69-74.
-
Lee, K.-M. and D. Zhou, "A Real-Time Optical Sensor for Simultaneous Measurement of 3-DOF Motions," IEEE/ASME Trans. on Mechatronics. September 2004, vol. 9 no. 3, pp. 499-507.
-
Foong, S.,K.-M. Lee, and K. Bai, "Harnessing Embedded Magnetic Fields for Angular Sensing with Nano-degree Accuracy," IEEE/ASME Trans. on Mechatronics. On-line: 05 April 2011, DOI: 10.1109/TMECH.2011.2119325.
-
Foong, S., K.-M. Lee and X. Chen, “Optimized Distributed Field-based Sensing for Control of Voice Coil Motor,” to appear in Proc. of ASME Dynamic Systems and Control Conference, October 31 –November 2, 2011, Arlington, Virginia.
Professor Kok-Meng Lee
George W. Woodruff School of Mechanical
Engineering
Georgia Institute of Technology
Atlanta, GA 30332-0405
Tel: (404)894-7402. Fax: (404)894-9342. Email:
kokmeng.lee@me.gatech.edu
http://www.me.gatech.edu/aimrl/
